Challenges for students as they interact with vocabulary in mathematics
While every discipline has its own unique set of vocabulary,
in mathematics vocabulary plays an especially important role. In mathematics vocabulary is not just used to
name objects but mathematical objects are actually brought into being through
definition of the object.
In this module we will consider the unique challenges of addressing mathematical vocabulary and will discuss some strategies that teachers can use to help students become more adept at interpreting and using mathematical vocabulary. For this module we will concept vocabulary as words and their definitions that are used to name mathematical objects. We will not consider syntactical issues surrounding the use of vocabulary.
In this module we will consider the unique challenges of addressing mathematical vocabulary and will discuss some strategies that teachers can use to help students become more adept at interpreting and using mathematical vocabulary. For this module we will concept vocabulary as words and their definitions that are used to name mathematical objects. We will not consider syntactical issues surrounding the use of vocabulary.
As students work to learn mathematics, they face some challenges in understanding and using mathematical vocabulary.
Challenge #1: Different types of vocabulary
One challenge that students face dealing with mathematics vocabulary is that there are really 3 types of vocabulary used in mathematics (Duru & Koklu, 2011). There are English words, used in expected and routine ways. There are English words used in ways that are very specific to mathematics. There are specialized mathematical terms, some of them identical to common English words. Consider, for example, the following passage:
A line segment is a diameter of a circle and only if it is a chord of the circle and subtends an arc of measure 180 degrees.
This short statement contains the following specialized mathematical vocabulary: line segment, diameter, circle, chord, subtend, arc, measure, degree. Of these, the word chord is one that is used in ordinary English with a very different meaning. Several other terms, particularly circle and arc, are mathematical in origin but are often used in everyday English in less the correctly mathematical ways. For example, we might describe the arc made by a football that has been kicked into the air or the arc created by a pearl necklace but neither of these curves is actually an arc – one is a parabolic curve and the other probably a catenary curve. This sentence also contains several ordinary English words and phrases that take on particular meaning in a mathematical context. For example, the phrase if and only if has a meaning here consistent with its ordinary English usage but, in addition, implies a specific mathematical condition of reflexivity. Even the word and may gain special significance when used in a mathematical context. In this context, the ordinary English use is sufficient but, in other settings, it may be necessary to read it as more akin to and at the same time.

The challenge for students in dealing with these different types of vocabulary is that students are often unclear about the type of vocabulary is being used in a given setting. So, in addition to learning the specialized vocabulary of mathematics, students must learn when particular words are being used a specialized sense and when they are being used in the ordinary English sense.
Challenge #2: Inconsistent Definitions
Precise definitions are critical to the very nature of mathematical endeavor. Mathematical objects are what they are because of the definition imposed upon them. For example, a triangle is not a triangle because it looks like one or because it functions as a triangle; it is a triangle because it fits the definition of a triangle. A triangle then has basic properties based on the definition and the mathematical assumptions behind this definition. If the definition or assumptions change, then the properties of the mathematical object change may change as well. So for example, if we change assumptions about the nature of plane and consider the surface of a sphere as our planar surface the familiar property that the sum of the measures of the angles in a triangle is 180 degrees is not longer correct. Instead, the sum of the measures of the angles must be greater 180 degrees. Contrast this role of definition with the role of definition in science. In science a substance exists and has certain properties. These properties may be included as part of the definition of the substance but changing the definition or the context of the definition does not change the properties of the substance. Water, at sea level, will freeze at 32 degrees Fahrenheit no matter how we choose to define water.
The central role that precision definitions play in creating mathematical objects means that any lack of precision or variation in definition can be particularly problematic in mathematics. Unfortunately, although definitions of mathematical terms are treated as precise and consistent, they are not always so. Consider, for a moment, the definition of a circle. According the Common Core State Standards for Mathematics, even a kindergarten student should be able to identify a circle. So, is the following figure a circle?
Precise definitions are critical to the very nature of mathematical endeavor. Mathematical objects are what they are because of the definition imposed upon them. For example, a triangle is not a triangle because it looks like one or because it functions as a triangle; it is a triangle because it fits the definition of a triangle. A triangle then has basic properties based on the definition and the mathematical assumptions behind this definition. If the definition or assumptions change, then the properties of the mathematical object change may change as well. So for example, if we change assumptions about the nature of plane and consider the surface of a sphere as our planar surface the familiar property that the sum of the measures of the angles in a triangle is 180 degrees is not longer correct. Instead, the sum of the measures of the angles must be greater 180 degrees. Contrast this role of definition with the role of definition in science. In science a substance exists and has certain properties. These properties may be included as part of the definition of the substance but changing the definition or the context of the definition does not change the properties of the substance. Water, at sea level, will freeze at 32 degrees Fahrenheit no matter how we choose to define water.
The central role that precision definitions play in creating mathematical objects means that any lack of precision or variation in definition can be particularly problematic in mathematics. Unfortunately, although definitions of mathematical terms are treated as precise and consistent, they are not always so. Consider, for a moment, the definition of a circle. According the Common Core State Standards for Mathematics, even a kindergarten student should be able to identify a circle. So, is the following figure a circle?
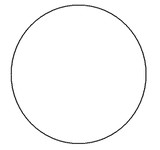
Remembering that in mathematics determinations about an object are based on definitions, we need to go the definition of a circle to answer this question. Take few moments and search the Internet for some definitions of a circle.
The first definition that comes up in my search is, "a round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center)." By this definition the figure above is a circle. However, a more classic definition of a circle is "the set of all points in a plane that are at a given distance from a given point, the center." By this definition, none of the blue part of the figure above is a circle. A circle itself is just the outside boundary of the figure shown above. For this definition, a figure like this would be a more correct representation.
Very often the contradictions involved in differing common definitions are not made evident to students. Students are taught to treat mathematical definitions as precise and authoritative but are confronted with examples like the following:
The definition of a circle is a curved line that is the same distance from the center all the way around and connects at the point where it began.
Although this definition is consistent with the second one given above, neither of the examples provided fits the definition. A plate is not a curved line. The earth is neither a curved line nor a circle. More correctly, a round plate is closer to being a disc while the earth is closer to being a sphere. So, in addition to learning the definitions of mathematical vocabulary words, students also need to learn to watch for subtle variations that may entirely change the nature of the object being defined.
The first definition that comes up in my search is, "a round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center)." By this definition the figure above is a circle. However, a more classic definition of a circle is "the set of all points in a plane that are at a given distance from a given point, the center." By this definition, none of the blue part of the figure above is a circle. A circle itself is just the outside boundary of the figure shown above. For this definition, a figure like this would be a more correct representation.
Very often the contradictions involved in differing common definitions are not made evident to students. Students are taught to treat mathematical definitions as precise and authoritative but are confronted with examples like the following:
The definition of a circle is a curved line that is the same distance from the center all the way around and connects at the point where it began.
- An example of circle is a round plate.
- An example of circle is the earth.
Although this definition is consistent with the second one given above, neither of the examples provided fits the definition. A plate is not a curved line. The earth is neither a curved line nor a circle. More correctly, a round plate is closer to being a disc while the earth is closer to being a sphere. So, in addition to learning the definitions of mathematical vocabulary words, students also need to learn to watch for subtle variations that may entirely change the nature of the object being defined.
Challenge #3: Density of Mathematical vocabulary
An additional challenge for students as they strive to learn math-specific vocabulary is the relative density of the use of such specific vocabulary. Seldom are definitions of mathematical objects stated without using multiple other vocabulary words. Consider, for example, this definition of a parabola: "a symmetrical open plane curve formed by the intersection of a cone with a plane parallel to its side." To understand this definition a student must be familiar with the mathematical terms: symmetrical, open, plane, curve, intersect, cone, and parallel.
An additional challenge for students as they strive to learn math-specific vocabulary is the relative density of the use of such specific vocabulary. Seldom are definitions of mathematical objects stated without using multiple other vocabulary words. Consider, for example, this definition of a parabola: "a symmetrical open plane curve formed by the intersection of a cone with a plane parallel to its side." To understand this definition a student must be familiar with the mathematical terms: symmetrical, open, plane, curve, intersect, cone, and parallel.

